Week 12 Discussion/Lab Notes

Administrivia

• Midterm 3 is next week (4-19). As with the other midterms, it's a week later than usual.
• Make sure you bring your textbook and a copy of mceval.scm to the exam.
• No one has been showing up to office hours in the past couple of weeks. The material is getting harder, so make use of them! Even if you don't have specific questions, you should go if you need anything clarified.
• By popular(?) demand, I will hold a review session on Tuesday at 7 pm in 306 Soda.

See also Brian Denny's notes on programming languages and his overview of the MCE.

The Big Picture

Up till now, we've been discussing the structure of computer programs. From this week onward we'll be dealing primarily with the interpretation of computer programs.

Keep in mind that just like everything else in this course, this is all about abstraction.

• Just as we used data abstraction to build larger and more complex data objects from smaller, simpler structures, we can use abstraction to build higher-level languages from lower-level ones. For example, we can start off with binary machine code, use it to implement an assembly language, use assembly to implement C, use C to implement Scheme, ...
  
  
• Just as we used procedures to abstract away details of computation, by using increasingly higher-level languages we can abstract away details of writing programs!

The Evaluator as a Black Box

What is a program? A program is essentially a description of some desired computational process.

We can think of an evaluator as a black box that takes this description and some data and produces some result.

This black box doesn't need to be physical; we can implement it as another program!

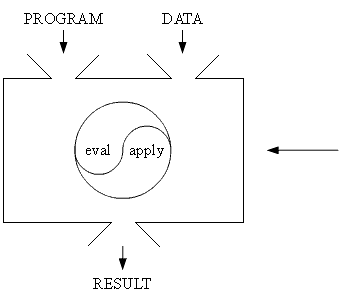The Evaluator: a program that evaluates the input program when applied to the input data

This is the pinnacle of data-directed programming. To the evaluator, the input program is just more data!

Some things to note:

• the input program can be in any language
• the evaluator can be implemented in any sufficiently powerful language

The language of the input program and the language used to implement the black box are independent. In our case, Scheme will be the language for both, and hence our evaluator is metacircular.

Unfortunately, because both languages are Scheme, this makes it very easy to confuse input code with the implementation code. This is probably the biggest cause for confusion. You must make an effort to keep them straight! If you think about the input program as data to the evaluator, distinguishing between them will be easier. (See Level Confusion, below.)

Why?

Why should we spend time studying and building evaluators? There are a number of reasons:

• At the most superficial level, building our own evaluator will allow us to change the syntax to the language. Don't like lambda? You can rename it to make-proc. Don't like prefix notation? You can change the language to use infix or postfix notation instead.
  
  
• Studying the metacircular evaluator will allow us to understand how it works. Understanding how the evaluator works helps us to understand the language better. And ultimately, a better understanding of the language allows us to write better programs!
  
  
• We can modify the evaluator to behave differently. For example, we can examine what would happen if Scheme used dynamic scope instead of lexical scope, or if it used normal-order evaluation instead of applicative-order.
  
  
• Studying Scheme evaluators will allow us to better understand how to write evaluators for other languages. With this power, we can invent our own languages specialized for particular tasks! For example, when we deal with logic programming in week 15, we'll be using a query language that's significantly different from Scheme.

Terminology

• underlying language--This is the below-the-line language we use to implement the evaluator itself. This is also referred to as the implementation language.
• meta language--This is the above-the-line language we feed into the evaluator. Also referred to as the source language or the implemented language.

Level Confusion

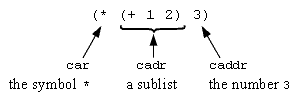
Suppose we are running the metacircular evaluator and we enter the expression (* (+ 1 2) 3). What is this expression from the below-the-line perspective? What does the underlying Scheme interpreter treat this as?

From the below-the-line perspective, things typed into the metacircular evaluator are either just atomic symbols or are lists of symbols. (Technically, symbols, numbers, booleans, strings, etc.) It's data. For example:

Remember this! This is the key to distinguishing meta-Scheme from the underlying Scheme. As another example, if we type (lambda (x) (* x x)) into the metacircular evaluator, we are typing in just a list whose car is the symbol lambda, whose caddr is the list (x), etc..

To emphasize this point further, consider how to invoke mc-eval directly from the underlying Scheme system:

   (mc-eval '(* (+ 1 2) 3) the-global-environment)

Furthermore, procedures in meta-Scheme are tagged lists to the underlying Scheme. The underlying Scheme system cannot invoke these "meta-procedures" directly!

Quick Review of Environment Diagrams

The first two evaluation rules are the most important:

• Every lambda expression creates a new procedure. Procedures are represented as bubble-pairs. The bubbles point to:
• the parameters and body of the procedure
• the frame in which the procedure was created
• Whenever a compound procedure is called:
1. Evaluate all the arguments before calling the procedure
2. Extend the environment of the procedure with a new frame
3. Bind values to the parameters of the procedure
4. Evaluate the body of the procedure

(By modifying these rules, we can change the behavior of the evaluator. For example, the rule about evaluating all the arguments before the procedure is called is necessary for applicative-order evaluation. If we get rid of it, we'll end up with a normal-order evaluator! Similarly, the rule about extending a procedure's environment is necessary for lexical scoping. Changing these rules will give us dynamic scoping.)

Below-the-line Representation

So given the environment diagramming rules, when we construct a meta-procedure, what do we need to store? They must have:

• a list of parameters
• a body
• a pointer to the defining environment

We can package these things together in a list. Meta-procedures are lists to the underlying Scheme system.

How can we implement environments? What is an environment? Recall that an environment is a chain--a sequence--of frames. The list data structure is perfect for this! Environments are lists of frames.

How about frames? Frames must store bindings. We can either maintain a list of names and a list of values, or we can have one big list of name-value pairs. The textbook uses the first method.

The core: mc-eval, mc-apply, driver-loop

mc-eval evaluates expressions by looking up variables, figuring out how to handle special forms, and by calling mc-apply on procedures.

Here's a simplified version of mc-eval without the complications from data abstraction. A lot of other details have been stripped away to give a better sense of the general structure:

   (define (mc-eval exp env)
     (cond ((number? exp) exp)
           <other self-evaluating cases>
           ((symbol? exp) <look up variable in env>)
           ((eq? (car exp) 'if)
            <use special evaluation rule for if>)
           ((eq? (car exp) 'lambda) <create a procedure>)
           <cases for other special forms>
           (else <invoke meta-procedure with mc-apply>) ))

mc-apply handles invocation of all meta-procedures. How do we invoke procedures? For primitive procedures we apply them "by magic." (Since primitives are created in the underlying Scheme system, the underlying system knows how to deal with them.) For compound procedures, again recall the environment diagramming rules:

1. Evaluate all the arguments before calling the procedure
2. Extend the environment of the procedure with a new frame
3. Bind values to the parameters of the procedure
4. Evaluate the body of the procedure

Here's a version of mc-apply with the details stripped away:

   (define (mc-apply procedure arguments)
     (cond ((primitive-procedure? procedure)
            <apply by magic>)
           ((compound-procedure? procedure)
            <extend the environment and bind values to parameters>
            <evaluate body with mc-eval>)
           (else <error, not a procedure>) ))

(Note that mc-eval handles the step about evaluating all the arguments before invoking a procedure.)

driver-loop merely provides a convenient interface to the evaluator by going through a read-evaluate-print loop. For example, we could invoke the evaluator explicitly:

   (user-print (mc-eval '(lambda (x) (* x x)) the-global-environment))

(Why do we need user-print?)

Things to ponder:

• If mc-eval and mc-apply perform mutual recursion by calling each other, when do they stop? What are the base cases for mc-eval? What are the base cases for mc-apply?
• Why does mc-eval need to take an environment as an argument?
• Why doesn't mc-apply need to take an environment as an argument?

Scoping: Lexical vs. Dynamic

In a lexically-scoped language, each procedure has some notion of its defining environment--the environment in which it was created. Furthermore, whenever a procedure is called, that procedure's defining environment is extended.

Lexical scoping often is referred to as static scoping. This means that code can be analyzed by the evaluator at compile-time--before it is actually evaluated. From this kind of analysis, we can determine what each variable refers to, and we can determine what the defining environment to each procedure is. Thus, when we invoke a procedure, we can know ahead of time which environment to extend. (Remember, in a lexically-scoped language, a given procedure, when invoked, always extends the same environment.)

In the long run, this means that lexical languages lead to faster code. The more things we can determine ahead of time, the fewer things we need to compute when the program is actually run, and the more optimizations we can make.

In contrast, in a dynamically-scoped language, whenever a procedure is called, the current environemnt is extended. Therefore we don't care what a procedure's defining environment is. (We can thus represent a procedure as a single "bubble" instead of as a bubble-pair.)

With dynamic scope, variable bindings are determined at run-time. This means that we have to explicitly lookup variables while we're running the program. Furthermore, since dynamic scope always extends the current frame for procedure calls, we can't garbage collect frames until the program terminates. For example, consider the following sequence of expressions:

   (define x 3)

   (define (foo x)
     (bar))

   (define (bar) x)

   (foo 4)

Using lexical scope, when we call (foo 4), we know that the resulting frame is no longer necessary and can be thrown away, because no procedure can ever access foo's local variable x.

In contrast, using dynamic scope, we must keep foo's frame, because bar can access it. Thus, dynamically-scoped languages use more memory than lexically-scoped ones.

The lecture notes discuss some more of the advantages and disadvantages of each scoping behavior.

What would we need to change in the metacircular evaluator for it to use dynamic scoping instead of lexical?

The fundamental change to the MCE is to mc-apply. Rather than calling extend-environment on the procedure's defining environment, we call it on the current environment instead. Of course, since mc-apply doesn't have a pointer to the current environment, we'll have to change mc-eval so that when it calls mc-apply, it supplies the current environment as an additional argument.

Here is the modified code for dynamic scoping: dyn-mce.scm.

(Those are the minimum changes required for the MCE to use dynamic scoping. We can note, however, that with dynamic scope a lot of the existing code is no longer necessary. For example, rather than passing the environment as an argument to mc-eval (and the other eval- procedures), we can maintain a global pointer to the current environment instead. (Why can't we do this with lexical scoping?))